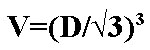Comment trouver le volume d'un parallélépipède?
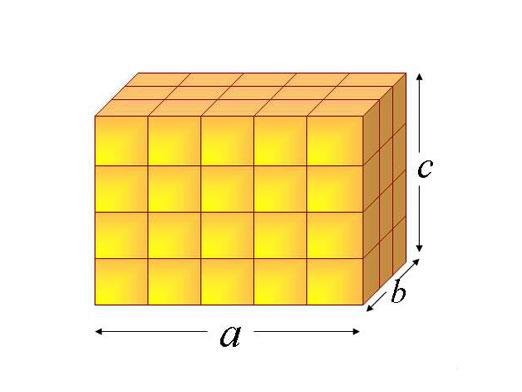
Un parallélépipède est une variante spéciale du prisme. Son unicité réside dans le fait qu'elle est constituée de faces de forme quadrangulaire, et que chaque paire de plans se faisant face est parallèle. Il y a plusieurs formules pour calculer le volume de cette figure: une méthode générale, aussi bien que quelques méthodes plus simples, applicables à des cas particuliers de cet hexaèdre.
Comment trouver le volume d'un parallélépipède? D'abord, vous devrez calculer la surface (S) de la base du parallélépipède. Par définition, les côtés opposés l'un à l'autre et formant ce plan sont parallèles, l'angle entre eux pouvant être quelconque. En conséquence, les faces de la place est le produit de la longueur des bords adjacents (a et b) par le sinus de l'angle entre eux (α): S = a * b * sin (α).
Ensuite, multipliez le résultat parla longueur du bord du parallélépipède (c), qui forme un angle avec les côtés a et b. Puisque la face latérale dont ce bord fait partie ne peut être perpendiculaire à la base de la figure, la valeur calculée doit être multipliée par le sinus de l'angle de face latérale (β): V = S * c * sin (β). En résumé, la formule de calcul du volume d'un parallélépipède ressemblera à ceci: V = a * b * c * sin (α) * sin (β).
Exemple:
A la base de la figure, une face avec les bords 15 et 25centimètres, dont l'angle est de 30 °, les faces latérales ont une inclinaison de 40 ° et un bord de 20 cm de longueur Le volume d'une telle figure est: 15 * 25 * 20 * sin (30 °) * sin (40 °) ≈ 7500 * 0, 5 * 0,643 ≈ 2411,25 cm3.
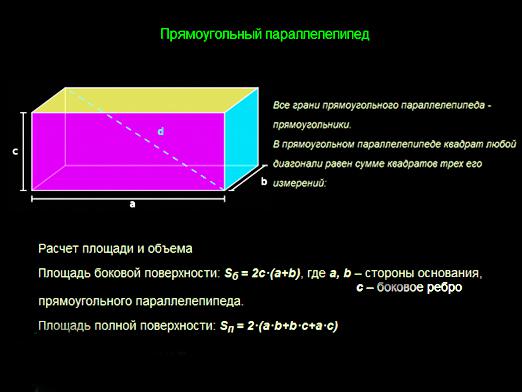
Comment trouver le volume d'un parallélépipède rectangle? Dans ce cas, la formule est considérablement simplifiée. Sinus de l'angle droit est l'unité, laissant tous les angles de formule, respectivement, il suffit de multiplier la longueur des nervures adjacentes ont un parallélépipède. Avec les nervures ont des longueurs données dans l'exemple précédent, le volume de la figure pour obtenir 15 * 25 * 20 = 7500 cm3.