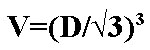Comment trouver la surface d'un cube?

Un cube est une version en trois dimensions d'un carré. Connaissant la longueur du bord du cube (a), on peut utiliser la formule la plus commune pour déterminer la surface (S). En partant du fait que l'aire du carré correspond à la longueur du carré érigé, et que le cube en a six, on obtient: S = 6 ∙ a². Cette formule détermine la zone de la surface totale du cube.
Méthodes pour déterminer la surface d'un cube
- Si le volume (V) de l'espace est donné, ce qui est délimité par les côtés du cube, et la longueur du bord est inconnue, alors la zone (S) est définie de cette manière.
Lorsque la seule taille de figure connue,est la longueur du bord surélevé du troisième bord, puis la dimension de la longueur du côté de chaque face du cube est déterminée en extrayant la racine du cube du paramètre existant. La formule de la surface du cube est: S = 6 ∙ (√√V) ².
- Lorsque la longueur diagonale de l'hexaèdre (L) est donnée, alorsla longueur d'une face peut être facilement calculée et, avec elle, l'aire de la figure. La diagonale est définie comme suit: L / v3. Et la surface du cube est donc calculée comme suit: S = 6 ∙ (L / √3) ² = 2 ∙ L², ce qui est très pratique pour les calculs.
- Comment trouver la surface d'un cube lorsque spécifiérayon de la sphère (R) décrit autour de l'hexaèdre? Simplement! Il suffit d'appliquer la formule: S = 8 ∙ R² = 2 ∙ (2 ∙ R) ². Ceci est possible grâce au fait que la diagonale du cube correspond au paramètre de diamètre de la sphère.
- Connaissant le rayon du cercle inscrit dans l'hexaèdre, la formule de la surface du cube s'écrit comme suit: S = 24 ∙ r².
Surface du cube
S = s1 + s2 + s3 + s4, dans lequel les termes sont quatre domaines de parallélogrammes, respectivement, qui forment la surface latérale du parallélépipède.
La formule de l'aire de la surface latérale du cube peut être représentée par S = P • h, pourvu qu'un parallélépipède rectiligne soit donné, avec un périmètre connu de la base P et de la hauteur h.
Lorsque les calculs doivent être faits sur un rectangleparallélépipède (toutes ses faces - rectangles) avec les longueurs connues des côtés de la base (D et C), lorsque les deux k - chiffre de bord latéral, tandis que la surface latérale du cube est définie par: S = 2 • k • (d + c).