Comment trouver les côtés d'un trapèze?

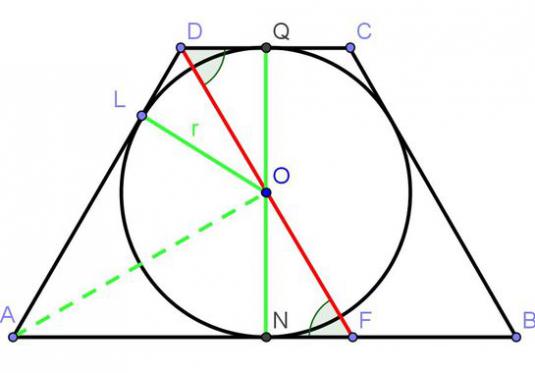
Le cours d'école de géométrie implique la connaissanceavec toutes sortes de quadrangles, y compris les trapèzes. Les tâches les plus élémentaires concernant les trapèzes sont la recherche de côtés et de captures. Dans cet article, nous allons examiner plusieurs exemples de résolution de problèmes sur la recherche des côtés d'un trapèze.

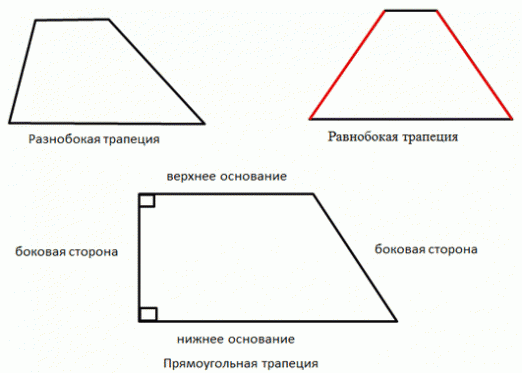
Trapezes sont:

arbitraire;
isocèles;
rectangulaire.

Résoudre des problèmes sur un trapèze arbitraire

Un trapèze est un quadrilatère à deuxles côtés sont parallèles et les deux ne le sont pas. La détermination du côté dans un trapèze arbitraire dépend des données initiales. Considérons le cas où les angles à la base et la hauteur sont connus.

Tâche 1

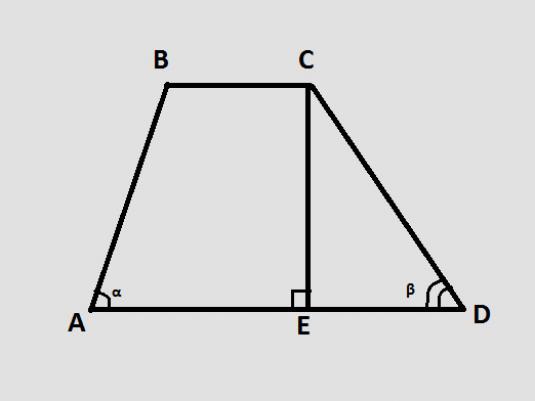
Un trapèze de l'ABCD est montré, dans lequel les hauteurs VC et CM sont faites égales à 6 cm Les angles à la base sont 60 et 45 degrés. Il est nécessaire de trouver les côtés.

Donc, nous avons deux triangles rectangles AVKet SDM, qui connaît une jambe et le coin opposé. Cynos (le rapport de la jambe opposée à l'hypoténuse) pour 60 et 45 degrés est connu: sin 60 = √3 / 2, et sin 45 = √2 / 2.

Nous obtenons:

sin 60 = BK / AB, d'où AB = VK / sin 60
AB = 6 / √3 / 2 = 4√3 (cm)
sin 45 = CM / SD, d'où le SD = CM / sin 45
LED = 6 / √2 / 2 = 6√2 (cm)

Réponse: AB = 4√3 cm et SD = 6√2 cm

La solution des problèmes sur un trapèze rectangulaire

Un rectangle est un trapèze dont les angles à l'un des côtés sont égaux à 90⁰. Considérons un exemple de la façon de trouver le côté d'un trapèze si les trois autres côtés sont connus.

Problème 2. Trois côtés sont donnés, dont l'un est perpendiculaire latéral.

Supposons qu'on nous donne un trapèze rectangulaire ABCD, dans lequel AB est perpendiculaire à BC. On sait que AB = 12 cm, BC = 1 cm, AD = 6 cm Il est nécessaire de trouver un grand côté latéral.

Solution:

A partir du point C, nous omettons la hauteur SK et obtenons le triangle rectangle KDK et le rectangle ABCD. Puisque les côtés opposés du rectangle sont CK = AB = 12 cm, et AK = BC = 1 cm.

Nous trouvons le segment KD:

CD = AD - AK = 6 - 1 = 5 (cm)

Selon le théorème de Pythagore:

LED²= SK²+ CD²= 12²5²= 144 + 25 = 169
LED = √169 = 13 (cm)

Réponse: LED = 13 cm

Problème 3. Étant donné les bases et l'angle à la base

Compte tenu de l'ABCD trapézoïdale, dans lequel les bases du soleil et la pression artérielle sont respectivement de 6 et 10 cm, l'angle de la VAD est droite, et le SDA est de 45 degrés. Trouvez le petit côté.

Nous dessinons la hauteur du SC et obtenons un triangle rectangulaire SKD et un rectangle ABCS. Puisque les côtés opposés du rectangle sont AK = BC = 6 cm.
CD = AD - AK = 10 - 6 = 4 cm
cos 45 = √2 / 2 = CD / LED, d'où le CD = CD / cos 45
Nous obtenons le SD = 4 / √2 / 2 = 4√2 (cm)

Réponse: SD = 4√2 cm

Résoudre les problèmes d'un trapèze isocèle

Le trapèze est appelé un isocèle, dont les côtés sont égaux. Pour comprendre comment les trouver, considérons les exemples suivants

Problème 4. Les bases et les hauteurs sont données

Étant donné un ABCD trapézoïde, dans lequel AB = SD et VC et CM - hauteurs. BC = 9 cm, AD = 19 cm et BK = CM = 12 cm Trouver le côté.

Prouvons que les triangles ABK et DSM sont égaux. Par la condition AB = CD, BK = CM. Puisque le trapèze est isocèle, les angles de BAC et SDM sont égaux. Puisque VC et CM sont des hauteurs, ces triangles sont rectangulaires. Cela signifie que l'angle ABK = 180 - (90 + VAK), et l'angle MSD = 180 - (90 + SDM), et que le VAK et le SDM sont égaux, alors AVK et MSD aussi. Ainsi, les triangles AVK et DSM et DSM sont égaux des deux côtés et l'angle entre eux.

Nous trouvons les segments AK et MD.

AK = MD = (AD - BC) / 2 = (19-9) / 2 = 5 (cm)

Par le théorème de Pythagore:

AB²= LED²= VC²+ AK²
AB²= LED²= 12²5²= 144 + 25 = 169
AB = √ 169 = 13 (cm)

Réponse: 13 cm.

Problème 5. Les deux bases sont données et un angle aigu

Étant donné un ABCD trapézoïde, dans lequel AB et SD sont égaux. BC = 12 cm, AD = 27 cm et angle à la base de 60 degrés. Trouvez le côté.

Nous dessinons la hauteur de la VC.

AK = (AD - BC) / 2 = (27-12) / 2 = 7,5 (cm)

cos 60 = AK / AB, donc AB = AK / cos 60
AB = 7,5 / 0,5 = 15 (cm)

Réponse: 15 cm

Problème 6. Le périmètre et la ligne médiane sont donnés.

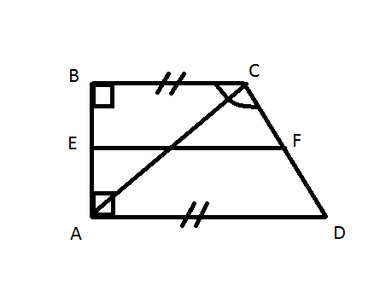
Un trapèze isocèle d'un ABCD est donné, dont le périmètre est égal à 80, et la ligne médiane du CM est sur le côté. Il est nécessaire de trouver le côté.

Il est connu de la condition que P = 2 x AB + BC + AD.

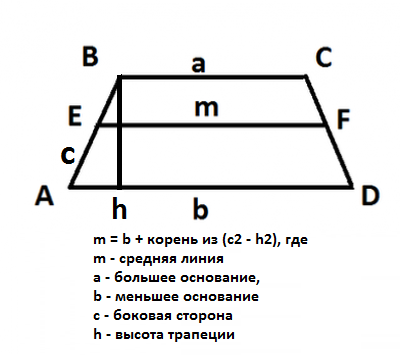
On sait que la longueur de la ligne médiane est égale à la moitié de la somme des bases, c'est-à-dire KM = (BC + AD) / 2. D'où BC + AD = 2 x AK = 2 x AB

Par hypothèse, CK = AB. Nous remplaçons toutes les données dans la formule périmétrique.

P = 2 x AB + 2 x AB = 80
4 x AB = 80
AB = 20 (cm)

Réponse: 20 cm

Comme on peut le voir à partir des exemples, la majorité des problèmes sur les trapézoïdes se résout à résoudre des problèmes sur des triangles rectangulaires.

Lisez plus: