Qu'est-ce qu'un sinus?

Qui d'entre nous n'a pas crié à l'école que les mathématiques luijamais utile. Il nous a semblé que toutes ces formules abstruses, ces équations encombrantes et ces noms complexes n'avaient rien à voir avec la vie réelle. Mais tôt ou tard, toutes les connaissances acquises à l'école trouvent leur application. Et sachant ce qu'un sinus, un cosinus ou une tangente peut sauver votre réputation.

Un peu de géométrie scolaire

Ainsi, le sinus est le rapport d'aspect dans un triangle rectangle. Rappelons en quoi consiste le triangle rectangulaire.

Angles. La somme des angles dans le triangle est de 180^o. L'angle avant est de 90^o. Par conséquent, les deux autres dans la somme devraient également donner 90^o. Autrement dit, nous avons un angle droit et deux angles vifs.

Parties. Le triangle rectangulaire est constitué d'une hypoténuse et de deux jambes. Deux jambes forment un angle droit, et l'hypoténuse se trouve en face d'elle.

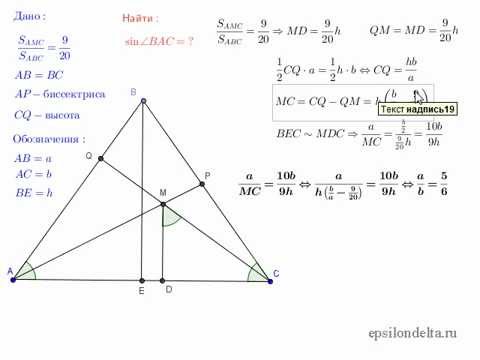
Quel est le sinus d'un angle? Comme déjà mentionné, ce ratio d'aspect. Mais lesquels? Le sinus d'un angle aigu est le rapport de la jambe, qui se trouve en face de cet angle, à l'hypoténuse. Considérez l'exemple:

Le sinus de l'angle A est le rapport du côté a (jambe opposée) au côté b (hypoténuse).

Le sinus de l'angle C est la relation latérale avec (le cathète se trouve du côté opposé C) au côté b (hypoténuse).

Autrement dit, si les côtés sont égaux à a = 3, c = 4, b = 5, alors le sinus de l'angle A sera 3/5, et le sinus de l'angle C sera 4/5.

Qu'est-ce que cela nous donne? Jusqu'à présent, rien, mais regardons un autre exemple. Augmentons le triangle en allongeant les côtés. Maintenant nous avons fait ceci:

Comme on peut le voir sur la figure, la longueur des côtés a augmenté, mais pas les coins. Mais ce qui est le plus intéressant - le rapport n'a pas changé non plus!

Supposons que d = 6, k = 8, m = 10. Alors le sinus de l'angle A est d / m = 6/10. Nous le coupons par deux côtés de l'équation et obtenons le même 3/5, comme dans le premier cas! Et peu importe comment vous changez, prolongez ou raccourcissez les parties, l'attitude des parties sera toujours la même.

Par conséquent, il est clair que le sinus est une valeur constante.

Et maintenant - trigonométrie

Les anciens Grecs ont remarqué cela pendant longtemps. Ils ont calculé les sinus des principaux coins et les ont enregistrés, afin de continuer à utiliser les quantités déjà prêtes, et de ne pas en inventer de nouvelles.

En plus du sinus, l'angle a aussi un cosinus(Le rapport de l'hypoténuse de la jambe adjacente), tan (relation opposée à une branche adjacente) et cotangente (accumbens rapport à une jambe opposée). Toutes ces valeurs sont appelées fonctions d'angle trigonométriques, et sont utilisés pour les calculs et résoudre des problèmes.

Mystérieuses tables de Bradys

Chaque fois que vous n'avez pas besoin de calculer le sinus. Il existe des tables de Bradis spécialement compilées, dans lesquelles tous les sinus, cosinus, tangentes et cotangents sont déjà enregistrés. De là, nous recevons des informations. Par exemple, si nous connaissons l'angle, nous connaissons son sinus et son cosinus. Inversement, si un sinus ou un cosinus est connu, on peut facilement trouver l'angle donné.

Naturellement, ces fonctions trigonométriques sont énormes. Rappelez-vous que tout est simplement impossible, mais pas vraiment nécessaire. Ils n'utilisent, pour l'essentiel, que quelques-uns d'entre eux.

Un peu sur les coins

Mais les fonctions trigonométriques ne sont pas seulementangles vifs et droits, ils sont aussi pour les stupides, mais ici pour leur découverte, un cercle et un graphique des axes de coordonnées seront déjà nécessaires. Et ceci est une histoire complètement différente.

Sinewave

Voyons maintenant ce qu'est une sinusoïde. Cela ressemble à une sinusoïde comme celle-ci:

Et est un graphique du changement de sinus dansen fonction du changement d'angle. Comme mentionné ci-dessus, les côtés peuvent changer, et l'angle reste le même - alors le sinus sera inchangé. Mais si l'angle change, le rapport d'aspect change et, par conséquent, la valeur sinusoïdale.

La sinusoïde affiche des changements numériques dans le sinusangle et est un graphique de la fonction y = sin (x). Il n'y a rien de compliqué ici, d'autant plus que les valeurs des sinus de tous les angles sont écrites dans les tables de Bradys. Mais nous ne nous souviendrons que des plus basiques.

Un peu plus sur la désignation des angles

Tout le monde sait que les angles sont mesurés en degrés ouradians. Degrés nous mesurons avec un rapporteur, qui ressemble à un demi-cercle. Un degré est 1/360 d'un cercle. Pourquoi ça? Parce que n'importe quel angle peut être "ouvert" ou "fermé". Vous pouvez même l'ouvrir pendant tout le tour et obtenir un cercle.

Chiffre d'affaires total, comme on le sait, 360^o. Une ligne droite est un angle de 180^o. Autrement dit, le diamètre du cercle est de 180^{à propos.} Ou le nombre Pi. Par conséquent, il se trouve que l'angle peut être aussi 90^o (en degrés), et Pi / 2 (en radians).

Maintenant, essayez de vous souvenir des sinus les plus basiques. Quels angles viennent immédiatement à l'esprit?

Angle direct - 90^o, Pi / 2 - sin = 1

L'angle déplié est de 180^o, Pi - sin = 0

Angle aigu de 60^o - Pi / 3 - sin = 0,866

Angle vif 45^o - Pi / 4 - sin = 0,7071