Comment trouver le sinus d'un angle?

Sinus (sin) est l'une des fonctions trigonométriques directes. Plus d'informations à ce sujet peuvent être trouvées dans notre article What is a sin.

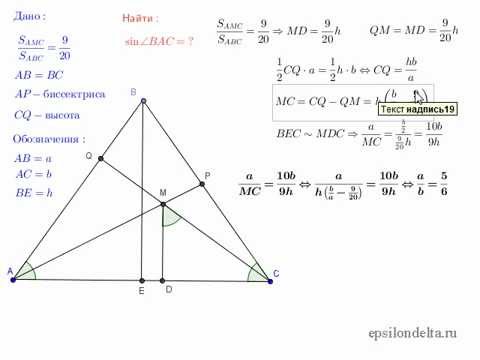
Sinus d'un angle dans un triangle rectangle

Avant de déterminer comment trouver le sinus d'un angle, vous devez définir les conventions. Supposons que dans un triangle rectangle:

• α est un angle aigu dont le sinus doit être trouvé;
• с - hypoténuse;
• b - cathète contigu;
• a est la jambe opposée.

Ensuite, pour trouver le sinus de l'angle aigutriangle rectangulaire, il suffit de calculer le rapport de la longueur de la jambe opposée à la longueur de l'hypoténuse: sin (α) = a / c. Il est bon de rappeler que le péché 90 ° est toujours 1.

Sinus d'un angle dans un triangle arbitraire

Trouver le sinus d'un angle dans un triangle arbitrairele plus facilement en utilisant le cosinus cosem (cos): le carré de la longueur de n'importe quel côté est égal à la somme des carrés des longueurs des deux autres côtés moins leur produit double par le cosinus de l'angle entre eux.

a² = b² + c² - 2 * b * c * cos (α)

A partir de cette formule, vous pouvez trouver le cosinus: cos (α) = (b² + c² - a²) / (2 * b * c)

Et puisque pour le même angle sin (α) ² + cos (α) ² = 1 et ceci est une constante, on peut dériver une formule pour déterminer le sinus:

sin (α) = √ (1 - cos (α) ²) = √ (1- (b² + c²-a²) ² / (2 * b * c) ²).

Plus en détail, trouver le sinus d'un angle en utilisant le cosinus est considéré dans notre article Comment trouver un sinus si le cosinus est connu.