Comment trouver le sinus du coin externe?

Les angles sinus doivent être calculés nonseulement dans un triangle rectangle, mais dans un autre. Pour ce faire, il est nécessaire de dessiner la hauteur du triangle (perpendiculaire à l'un des côtés, abaissé du coin opposé) et résoudre le problème comme pour un triangle rectangle, en utilisant comme une des jambes la hauteur.
Comment trouver le sinus du coin externe d'un triangle
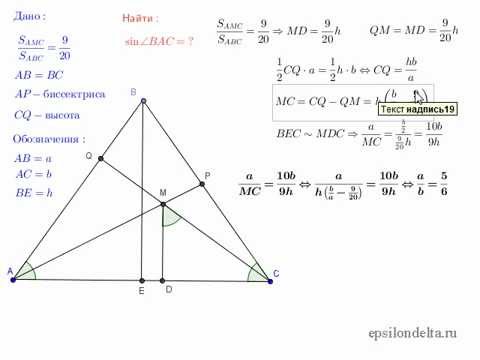
Vous devez d'abord comprendre ce qu'est un coin externe. Nous avons un triangle arbitraire ABC. Si l'un des côtés, par exemple AC, continue au-delà de l'angle BAC et dessine un faisceau AO, alors le nouvel angle OAB sera externe. Ici nous allons chercher son sinus.
Pour résoudre le problème, nous devons faire tomber la perpendiculaire BH sur le côté de l'UA à partir de l'angle ABC. C'est la hauteur du triangle. Le cours de la solution du problème dépendra de ce que nous savons.
L'option la plus simple est si vous connaissez l'angle de vous. Ensuite, le problème est résolu extrêmement facilement. Puisque le rayon OC est une ligne droite, l'angle OAC = 180 °. Par conséquent, l'angle OAB et BAC sont adjacents, et les sinus des angles adjacents sont d'amplitude égale.
Considérons un autre problème: dans un côté est connu triangle ABC arbitraire: AB = a et la hauteur BH = h. Nous devons trouver le sinus de l'angle du CCA. Étant donné que nous obtenons maintenant un triangle AVN, sinus de l'angle AVN est égal au rapport jambe VN à l'hypoténuse AB:
- sinBAH = BH / AB = h / a.
C'est aussi facile. Un problème plus compliqué, si la hauteur h est connue et les côtés AC = c, BC = b, il faut trouver le sinus de l'angle OAB.
Par le théorème de Pythagore, nous trouvons le cathéter du CH du triangle VSN:
- BC² = BH² + CH² b² = h² + CH²,
- CH² = b² - h², CH = √ (b² - h²).
De là, vous pouvez trouver un segment du côté AS de l'AC:
- AH = AC - CH = c - √ (b² - h²).
Maintenant, nous utilisons de nouveau le théorème de Pythagore pour trouver le troisième côté du triangle AV ABN:
- AB² = BH² + AH² = h² + (c - √ (b² - h²)) ².
Le sinus de l'angle BAC est égal au rapport de la hauteur de la HV du triangle sur le côté AB:
- sinBAC = BH / AH = h / (c - √ (b² - h²)).
Puisque les angles OAB et BAC sont adjacents, leurs sinus sont d'amplitude égale.
Ainsi, en combinant le théorème de Pythagore, la définitionsinus et quelques autres théorèmes (en particulier, sur des angles adjacents), il est possible de résoudre presque la majorité des problèmes sur les triangles, y compris trouver le sinus de l'angle externe. Parfois, des constructions supplémentaires peuvent être nécessaires: dessiner une hauteur à partir de l'angle désiré, continuer le côté du coin au-delà de ses limites, et ainsi de suite.